JoeyDDong's Blog
AtCoder Beginner Contest 384 Summary
JoeyDDong
  2024-12-15   2025-01-04  2.7k Words  12 Mins

本文是 AtCoder Beginner Conteset（ABC）384 的总结笔记。

A - aaaadaa

Problem：A - aaaadaa

签到题。将字符串中不是 a 的字符全部改成 b。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// Problem: https://atcoder.jp/contests/abc384/tasks/abc384_a

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;

int n;
char a, b;
string s;

void solve() {
    cin >> n >> a >> b >> s;
    for (auto& x : s)
        if (x != a)
            x = b;

    cout << s << endl;
}

int main() {
    cin.tie(0);
    ios_base::sync_with_stdio(false);
    solve();
    return 0;
}

B - ARC Division

Problem：B - ARC Division

模拟题。

按照题目要求做条件判断即可。

  • 如果参加的是 div1 并且当前 rating 在之间，就可以计入成绩
  • 如果参加的是 div2 并且当前 rating 在之间，就可以计入成绩
  • 其他情况直接跳过
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
// Problem: https://atcoder.jp/contests/abc384/tasks/abc384_b

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;

int n, r;
int d, a;

bool check_div1(int r) {
    if (r >= 1600 && r <= 2799)
        return true;
    return false;
}
bool check_div2(int r) {
    if (r >= 1200 && r <= 2399)
        return true;
    return false;
}

void solve() {
    cin >> n >> r;
    for (int i = 1; i <= n; i++) {
        cin >> d >> a;
        // 参加 div1，并且 rating 在 [1600,2799] 之间
        if (d == 1 && check_div1(r))
            r += a;
        // 参加 div2，并且 rating 在 [1200,2399] 之间
        else if (d == 2 && check_div2(r))
            r += a;
        // 否则跳过
        else
            continue;
    }
    cout << r << endl;
}

int main() {
    cin.tie(0);
    ios_base::sync_with_stdio(false);
    solve();
    return 0;
}

C - Perfect Standings

Problem：C - Perfect Standings

位运算 + STL

题目：

A B C D E 题分别对应 a b c d e 五个分值。

从只做出 A 题到全部做完 ABCDE ，共有 31 种组合情况。

按照分值从大到小输出各种做题的可能性，分值相同的时候，按照字典序输出。

思路：

这道题虽然使用最暴力的手工枚举也可以做，但是太过麻烦。下面是更加通用的方法。

需要解决两个问题：

  1. 如何枚举所有的做题状态？

    本题总共有五位，所以可以使用一个五位的二进制数就可以枚举出各个题的解答状态。

  2. 如何按照分数降序 和 字典序升序的方式排列。

    使用 struct 的时候，单独定义 cmp 比较算子。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
// Problem: https://atcoder.jp/contests/abc384/tasks/abc384_c

// 位运算
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;

int a[5];

struct Score {
    int s;       // 存储分值
    int st;      // 存储二进制状态
    string str;  // 存储对应的做题方案
} s[50];

// 自定义算子
bool cmp(const Score& a, const Score& b) {
    if (a.s != b.s) {
        return a.s > b.s;  // s 不同时按 s 降序
    }
    return a.str < b.str;  // s 相同时按 str 字典序升序
}

// 将二进制状态转化为字符串
string make_str(int x) {
    string s = "";
    for (int i = 0; i < 5; i++)
        if (x >> i & 1)
            s += 'A' + i;
    sort(s.begin(), s.end());
    return s;
}

// 计算当前二进制状态的分值
int cal_score(int x) {
    int res = 0;
    for (int i = 0; i < 5; i++)
        if (x >> i & 1)
            res += a[i];
    return res;
}

void solve() {
    // 读入各个题目的分值
    for (int i = 0; i < 5; i++)
        cin >> a[i];

    // 遍历所有 32 种状态，同时计算 分值 和 对应的字符串
    for (int i = 0; i <= 31; i++) {
        s[i].st = i;
        s[i].s = cal_score(i);
        s[i].str = make_str(i);
    }

    // 排序
    sort(s, s + 32, cmp);

    // 输出结果（只输出前 31 个结果，第 32 个结果是空集，跳过）
    for (int i = 0; i < 31; i++)
        cout << s[i].str << endl;
}

int main() {
    cin.tie(0);
    ios_base::sync_with_stdio(false);
    solve();
    return 0;
}

D - Repeated Sequence

Problem：D - Repeated Sequence

思维题

题目：

给定长度为的序列。以这组序列为模板，无限重复循环。

是否能截取连续出子序列，使和恰好为。

约束条件

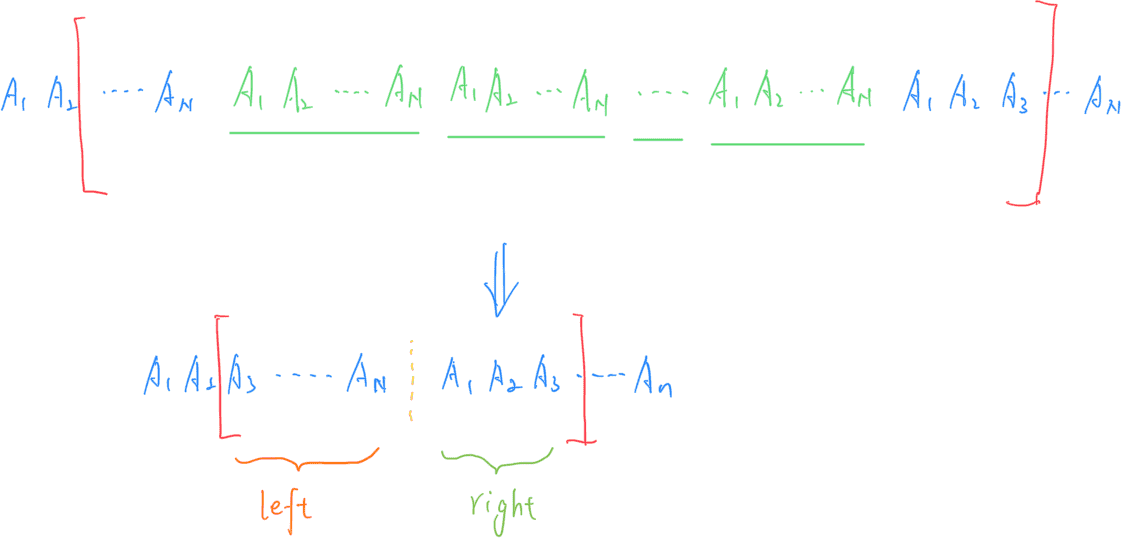
思路：

根据下图示例，我们可以发现，选取的子段由三部分组成：一个后缀，若干个周期 pattern，一个前缀。

由于任意的都是正数，所以我们可以直接知道可以有多少个完整的 pattern，即。

如果去除中间重复的 pattern，最后一定会剩下左边的一部分 left 和右边的一部分 right。那么

问题转化为，能不能找到一个后缀和一个前缀，使二者的和等于。

image-20241215194610477

最后剩下的部分，和的范围应该是。

所以我们依次遍历左边部分的后缀和，同时维护一个 set，判断 set 里面有没有我们想要的值即可。总时间复杂度为。（或者也可以直接使用二分，也可以达成相同的目的）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
// Problem: https://atcoder.jp/contests/abc384/tasks/abc384_d

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;

const int N = 2e5 + 10;
int A[N];
LL sum[N];
LL n, s;
set<LL> h;

void solve() {
    // 读入数据，维护 前缀和 和 set
    cin >> n >> s;
    for (int i = 1; i <= n; i++) {
        cin >> A[i];
        sum[i] = sum[i - 1] + A[i];
        h.insert(sum[i]);
    }

    s %= sum[n];
    sum[n + 1] = sum[n];
    bool can = false;

    // 从后往前逐个遍历
    for (int i = n + 1; i >= 1; i--) {
        // 计算出后缀和
        LL left = sum[n + 1] - sum[i - 1];
        // 计算出期待的前缀和
        LL right = s - left;
        // 看是否存在
        if (h.count(right))
            can = true;
        if (h.count(right + sum[n]))
            can = true;
        if (can)
            break;
    }
    if (can)
        cout << "Yes" << endl;
    else
        cout << "No" << endl;
}

int main() {
    cin.tie(0);
    ios_base::sync_with_stdio(false);
    solve();
    return 0;
}

E - Takahashi is Slime 2

Problem：E - Takahashi is Slime 2

优先队列 BFS。本题和 ABC 383 的 E - Sinking Land 题目非常相似。

题目：

给定的网格。每个网格中有一个数值。起始点位于。

从起点向四方向移动。只有数值严格小于当前累计值 res 的的时候，才能吃掉这个格子。

求最大累加值。

约束条件：

思路：

标准的优先队列 BFS 题目。按照题目写即可。

需要注意的一个细节点：

​ 题目要求“数值严格小于当前累计值 res 的的时候，才能吃掉这个格子”。这里的严格小于应该如何处理。如果直接写 s * X < res 的话，在本题规模下会溢出。这里只需要计算即可。代码写作 s < (res+X-1)/X 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
// Problem: https://atcoder.jp/contests/abc384/tasks/abc384_e

// 优先队列 BFS
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;

int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
const int N = 510;
LL g[N][N];
LL P, Q;
LL H, W, X;
LL res;
bool st[N][N];

// 创建结构体
struct Node {
    LL x, y, score;
    // 重置小于符号（为小根堆做准备）
    bool operator<(const Node& a) const { return score > a.score; }
};
priority_queue<Node> que;

void solve() {
    // 读入数据
    cin >> H >> W >> X >> P >> Q;
    for (int i = 1; i <= H; i++)
        for (int j = 1; j <= W; j++) {
            cin >> g[i][j];
        }

    // 初始化
    que.push((Node){P, Q, g[P][Q]});
    st[P][Q] = true;
    res = 0;

    // 优先队列 BFS
    /*
        注意：题目中要求，吸收单元格的 score 值必须严格小于 res/X
        这里直接使用上取整，即 score <(res+X-1)/X 即可满足要求
    */
    while (que.size() && (res == 0 || que.top().score < (res + X - 1) / X)) {
        Node now = que.top();
        que.pop();
        res += now.score;
        for (int i = 0; i < 4; i++) {
            int a = now.x + dx[i], b = now.y + dy[i];
            // 越界
            if (a < 1 || a > H || b < 1 || b > W)
                continue;
            // 已经被看过了
            if (st[a][b])
                continue;

            // 加入优先队列
            que.push((Node){a, b, g[a][b]});
            st[a][b] = true;
        }
    }

    // 输出结果
    cout << res << endl;
}

int main() {
    cin.tie(0);
    ios_base::sync_with_stdio(false);
    solve();
    return 0;
}

F - Double Sum 2

Problem：F - Double Sum 2

数论题目。（这道题非常的抽象，很难理解）

题目：

给定正整数。定义：只要还是偶数，就让他一直除以，最终剩下的值作为的结果。

给定序列，求的值。

约束条件：

思路：

技巧：
统计顺序的更改。核心思想：本题要求出个数字的和，如果一个个统计，肯定会超时。可以把数字分成组，一次算出一组的和，最后再相加。

整体思路：

  1. 定义为满足下面条件的所有对应的的总和
  • 条件 1：
  • 条件 2：是的倍数

​ 也就是说，是所有满足的配对的的总和。

  1. 那么，如果恰好能被整除的的和为。

​ 备注：这里可能稍微有点难理解。举个例子，一个数如果能被整除，那么它一定能被整除。那么只能被 8 整除的部分的总和就是

  1. 最终所求的答案就是：将所有的这种“刚好被除以次”的和，在分别除以后再累加起来，即。

细节问题处理：

根据上面的思路，于是问题就转变为：如何快速的求出的值？

我们可以知道：，如果直接双层遍历，时间复杂度是，显然不行。

技巧：同余条件等价于也就等价于。

所以当处理 j 位置时，我们希望知道：

  • 在的部分中，有多少个满足
  • 在的时候，若能够被整除，则这一对也要计入

为了方便计数求和，我们可以用一个以为键的 “字典 map” 来维护已经出现过的的计数和总和。

map：

  • 键 key：
  • 值 value：在当前余数下出现的所有的个数和总和

因此，当我们要处理时，先计算出，然后在 map 中查找这个 key 是否存在。

若存在，就可以得到相匹配的（满足条件的个数） 和（满足条件的和），就可以快速求出。

然后根据前面的公式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
// Problem: https://atcoder.jp/contests/abc384/tasks/abc384_f

#include <bits/stdc++.h>
using namespace std;
// typedef long long LL;
#define int long long  // 本题中大量使用 ll，为了方便直接定义为 int
typedef pair<int, int> PII;

const int N = 2e5 + 10, M = 2e7 + 10;
int n;
int a[N];
int sum[M];  // 存储累计和，A_i的上限是2e7，所以mp的idx不会超过这个数
int cnt[M];  // 存储计数
int d[30];   // 存储所有中间的 d 值

void solve() {
    // 读入原始数据
    cin >> n;
    for (int i = 1; i <= n; i++)
        cin >> a[i];

    int k = 1;  // 即 2^0
    // 遍历阶次
    for (int j = 0; j <= 24; j++) {
        // 从头遍历数组中的每个数
        for (int i = 1; i <= n; i++) {
            int key = a[i] % k;
            // mp[r]是a[i]%k后余数为r的所有数a[i]的累计和
            sum[key] += a[i];
            // cnt[r]是a[i]%k后余数为r的所有数出现次数
            cnt[key]++;
            // 累计获得 d_j 的值
            d[j] += sum[(k - a[i] % k) % k] + a[i] * cnt[(k - a[i] % k) % k];
        }
        // mp 与 cnt 重置
        for (int i = 1; i <= n; i++) {
            int key = a[i] % k;
            sum[key] = 0;
            cnt[key] = 0;
        }
        k = k * 2;
    }

    // 计算出结果
    int res = 0;
    k = 1;
    for (int i = 0; i <= 24; i++) {
        res += (d[i] - d[i + 1]) / k;
        k *= 2;
    }
    cout << res << endl;
}

signed main() {
    cin.tie(0);
    ios_base::sync_with_stdio(false);
    solve();
    return 0;
}
AtCoder Beginner Contest 384 Summary
2024/blog/54122/
Author
JoeyDDong
Published
2024-12-15 20:35
License
  1. A - aaaadaa
  2. B - ARC Division
  3. C - Perfect Standings
    1. 题目：
    2. 思路：
  4. D - Repeated Sequence
    1. 题目：
    2. 约束条件
    3. 思路：
  5. E - Takahashi is Slime 2
    1. 题目：
    2. 约束条件：
    3. 思路：
  6. F - Double Sum 2
    1. 题目：
    2. 约束条件：
    3. 思路：
  1. A - aaaadaa
  2. B - ARC Division
  3. C - Perfect Standings
    1. 题目：
    2. 思路：
  4. D - Repeated Sequence
    1. 题目：
    2. 约束条件
    3. 思路：
  5. E - Takahashi is Slime 2
    1. 题目：
    2. 约束条件：
    3. 思路：
  6. F - Double Sum 2
    1. 题目：
    2. 约束条件：
    3. 思路：