本文介绍了树状数组 BIT（Binary Indexed Tree）相关的基础算法知识。

1. 基础知识

参考链接：https://www.bilibili.com/video/BV1pE41197Qj

1.1 问题引入：

如果给定一个长度为的数组，要完成下面两个操作：

将第个数加上
输出区间 [x,y] 内每个数的和

我们可以对比一下几种方法实现的时间复杂度：

朴素方法：
- 单点修改：
- 求区间和：
- 进行n次操作，时间复杂度最坏是
前缀和方法：
- 单点修改：
- 求区间和：
- 进行n次操作，时间复杂度最坏是
树状数组方法：
- 单点修改：
- 求区间和：
- 进行n次操作，时间复杂度为，就可以处理非常大规模的数据了

从上面的三个对比可以知道，树状数组在执行需要的大量特殊操作的时候，具有时间复杂度的优势。

1.2 lowbit 操作：

表示非负整数n在二进制表示下，最后一个1及后面的0一起构成的数值

一般有两种写法：

        C++
        
      
int lowbit(int x){
    // 写法1: 一般采用这个写法
    return x & -x;
    // 写法2：
    // return x & (~x+1);
}

2. 树状数组

2.1 基本概念：

构建下面这样的数组 t 为树状数组：

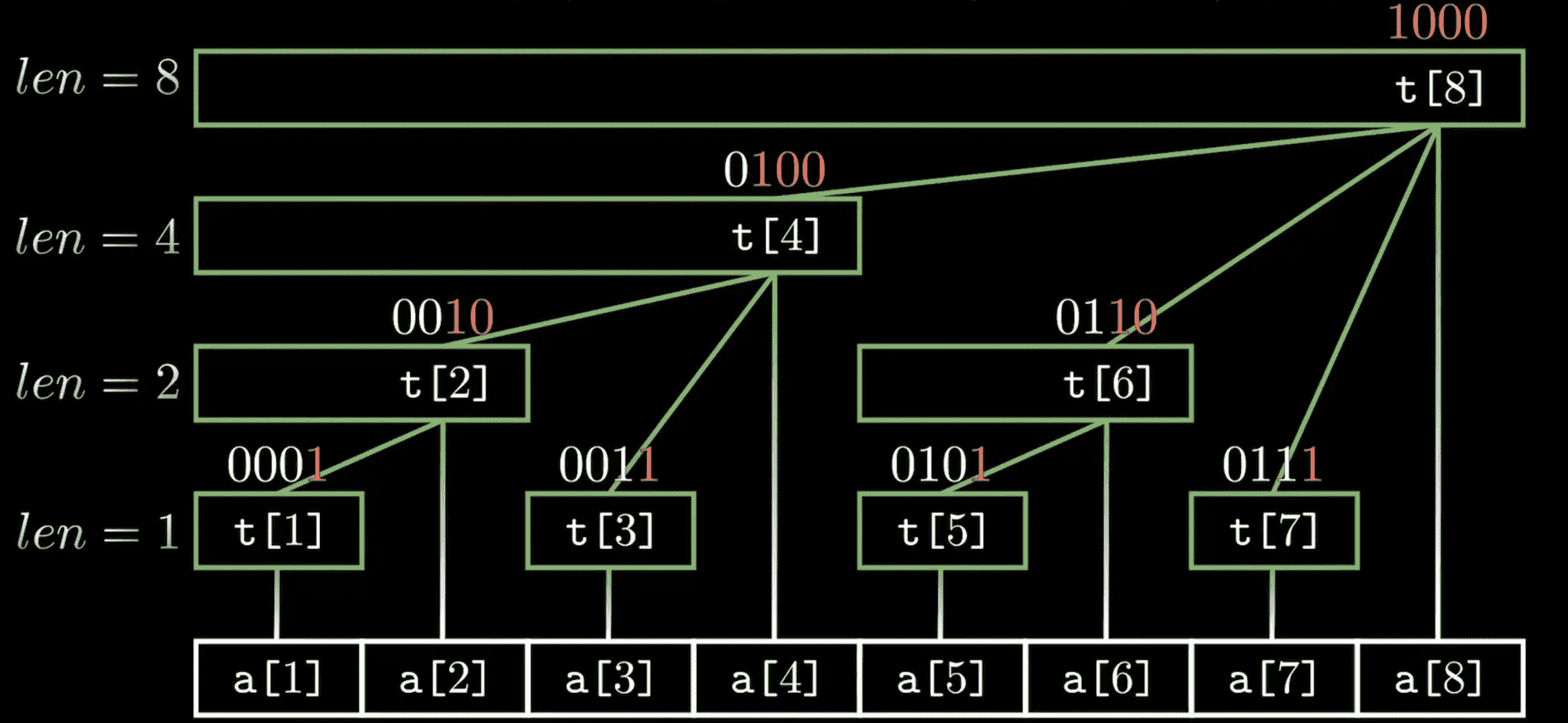
树状数组 t 有下面的性质：

t[x] 保存以x为根的子树中叶节点值的和
t[x] 节点的长度等于 lowbit(x)
t[x] 节点的父节点为 t[x+lowbit(x)]

整棵树的深度为

2.2 基本操作：

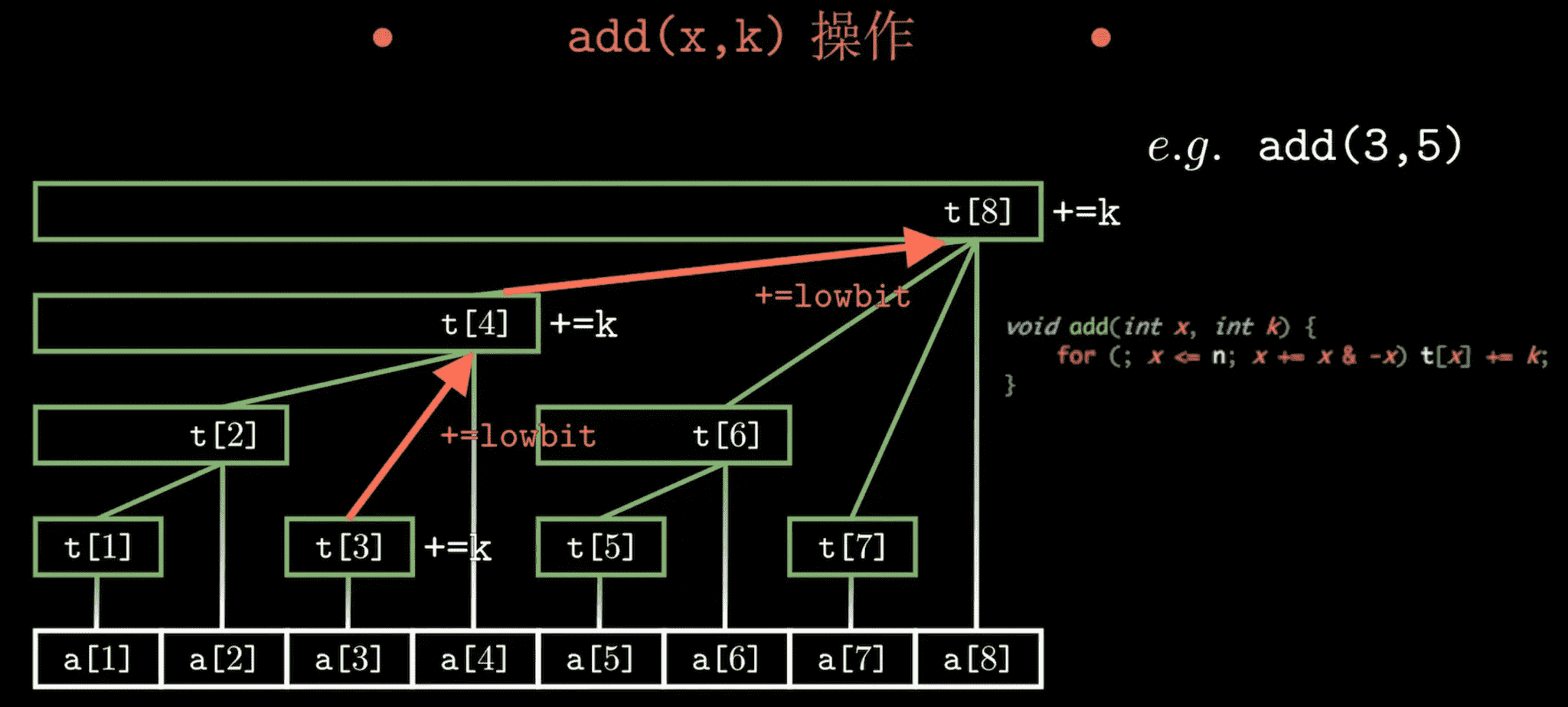
操作1：add(x,k)

即给第 x 个数加上 k。
例如：给 A[3] 加上 k。逐级向上都加上 k。

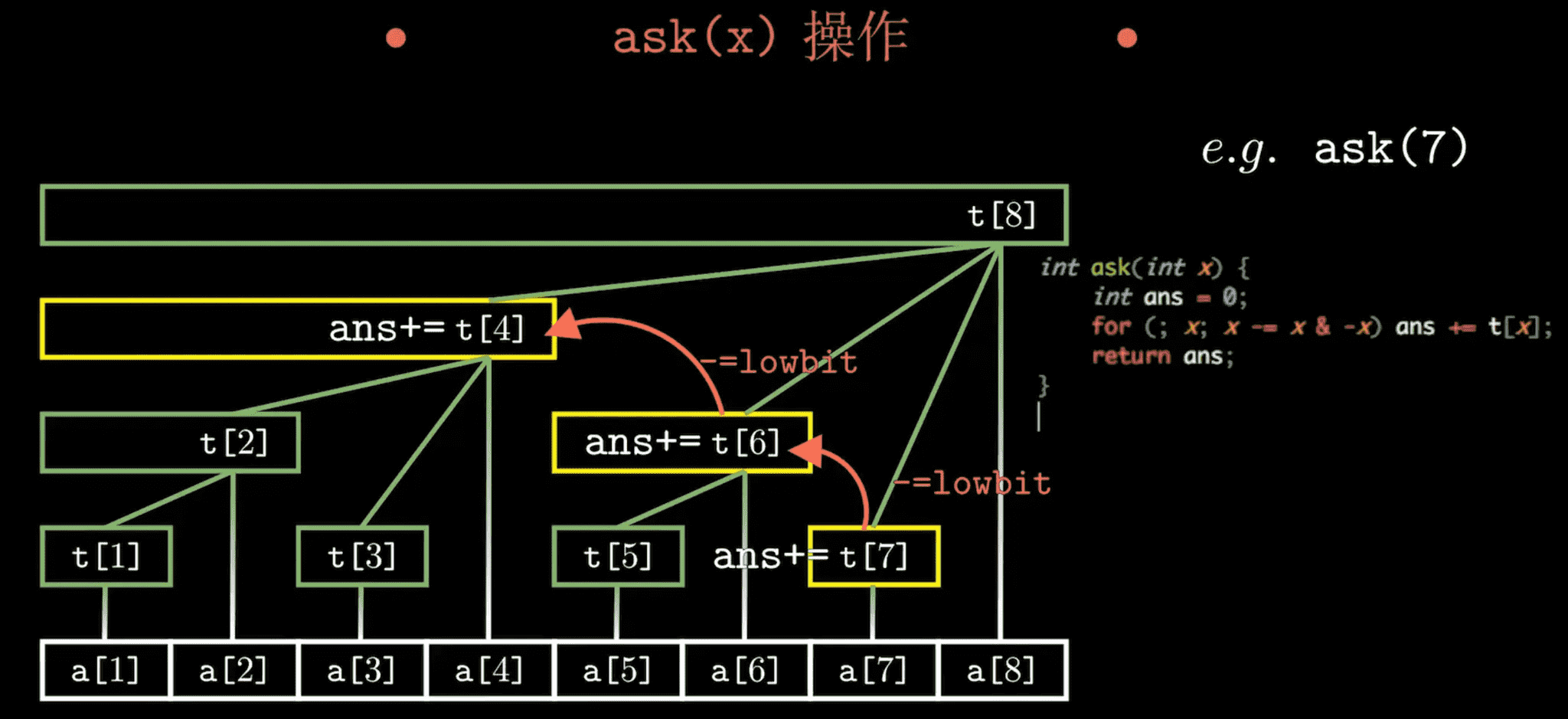
操作2：ask(x)

查询 x 的前缀和。
例如：查询前缀和 S[7] 的值，就从 t[7] 开始逐级向上加。

2.3 初始化：

已经给定了一个普通的数组 A，如何将它装进树状数组呢？

方法1: 使用 add 一个个装

最简单的方法，时间复杂度为

        CPP
        
      
for (int i; i <= n; i++)
    add(i, A[i]);

方法2: 使用 trick

时间复杂度为

先计算出来A的前缀和 S，再套下面的公式

        CPP
        
      
for( int i =1 ;i <= n ; i++)
    tr[i] = S[i] - S[i-lowbit(i)];

2.4 能应用的问题：

单点修改，区间查询

维护标准的树状数组即可。

单点修改：

x 位置加上 d，只需要 add(x,d) 即可

区间查询：

查询 [l,r] 的区间和，只需要 ans = ask(r) - ask(l-1) 即可

区间修改，单点查询

引入差分数组 b，用树状数组维护 b 的前缀和，即 a[] 每个元素的增量。

区间修改：

[l,r]+d 操作，只需要：add(l,d), add(r+1,d) 即可

单点查询：

查询 a[x]，只需要 ans = a[x] + ask(x) 即可

区间修改，区间查询

3. 例题

P3374 【模板】树状数组 1

Problem：P3374 【模板】树状数组 1

非常标准的单点修改，区间查询例题。

        C++
        
      
#include <iostream>
using namespace std;
const int N = 5e5+10;

int n,m;
int tr[N];

int lowbit(int x){
    return x & -x;
}

// 单点修改
void add(int x , int k){
    for(int i = x ; i <= n ; i += lowbit(i))
        tr[i] += k;
}

// 查询前缀和
int sum(int x){
    int res = 0;
    for(int i = x ; i ; i -= lowbit(i) )
        res += tr[i];
    return res;
}

int main(){
    // 读入数据
    cin >>n>>m;
    // 树状数组初始化
    for(int i = 1 ; i <= n ; i++){
        int x; cin >>x;
        add( i , x);
    }

    // 对应每个查询
    while(m--){
        int c;cin >>c;
        // 执行 add 操作
        if( c == 1){
            int x,k; cin >>x>>k;
            add(x,k);
        }
        // 执行区间求和操作
        else{
            int x ,y; cin >>x>>y;
            cout << sum(y) - sum(x-1) <<endl;
        }
    }
}

P3368 【模板】树状数组 2

Problem：P3368 【模板】树状数组 2

非常标准的区间修改，单签点查询例题。

        C++
        
      
#include <iostream>
using namespace std;
const int N = 5e5 + 10;

int n, m;
int tr[N];  // 这本题中，树状数组扮演了差分数组的角色
int a[N];

int lowbit(int x) {
    return x & -x;
}

// 单点修改
void add(int x, int k) {
    for (int i = x; i <= n; i += lowbit(i))
        tr[i] += k;
}

// 查询前缀和
int sum(int x) {
    int res = 0;
    for (int i = x; i; i -= lowbit(i))
        res += tr[i];
    return res;
}

int main() {
    // 读入数据
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        cin >> a[i];
    // 初始化树状数组（差分数组）
    for (int i = 1; i <= n; i++)
        add(i, a[i] - a[i - 1]);

    // 对应每个查询
    while (m--) {
        int c; cin >> c;
        // 区间修改操作
        if (c == 1) {
            int x, y, k; cin >> x >> y >> k;
            add(x, k), add(y + 1, -k);
        }
        // 单点查询（差分数组的前缀和）
        else {
            int x; cin >> x;
            cout << sum(x) << endl;
        }
    }
}